problem solving examples motion

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Request a Demo
• Get A Quote
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Lab Equipment
• Lab Procedures
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Making an Ion Concept Checker
• Phase Changes Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Chemical Reactions Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Task Tracker Directions
• Conceptual Physics Course
• On-Level Physics Course
• Honors Physics Course
• Chemistry Concept Builders
• All Chemistry Resources
• Users Voice
• Tasks and Classes
• Webinars and Trainings
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• Measurement and Calculations
• Elements, Atoms, and Ions
• Compounds,Names, and Formulas
• The Modern Atomic Model
• Chemical Bonding
• The Mole and its Applications
• Chemical Reactions
• Stoichiometry
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Solution Guide Corrections
• Motion in One Dimension
• Work, Energy and Power
• Chemistry of Matter
• Measurement and the Metric System
• Early Atomic Models
• Names and Formulas
• The Modern Model of the Atom
• Algebra Based On-Level Physics
• Honors Physics
• Conceptual Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Sample Problems and Solutions
• Kinematic Equations Introduction
• Solving Problems with Kinematic Equations
• Kinematic Equations and Free Fall
• Kinematic Equations and Kinematic Graphs

Check Your Understanding

Answer: d = 1720 m

Answer: a = 8.10 m/s/s

Answers: d = 33.1 m and v f = 25.5 m/s

Answers: a = 11.2 m/s/s and d = 79.8 m

Answer: t = 1.29 s

Answers: a = 243 m/s/s

Answer: a = 0.712 m/s/s

Answer: d = 704 m

Answer: d = 28.6 m

Answer: v i = 7.17 m/s

Answer: v i = 5.03 m/s and hang time = 1.03 s (except for in sports commericals)

Answer: a = 1.62*10 5 m/s/s

Answer: d = 48.0 m

Answer: t = 8.69 s

Answer: a = -1.08*10^6 m/s/s

Answer: d = -57.0 m (57.0 meters deep) 

Answer: v i = 47.6 m/s

Answer: a = 2.86 m/s/s and t = 30. 8 s

Answer: a = 15.8 m/s/s

Answer: v i = 94.4 mi/hr

Solutions to Above Problems

d = (0 m/s)*(32.8 s)+ 0.5*(3.20 m/s 2 )*(32.8 s) 2

Return to Problem 1

110 m = (0 m/s)*(5.21 s)+ 0.5*(a)*(5.21 s) 2

110 m = (13.57 s 2 )*a

a = (110 m)/(13.57 s 2 )

a = 8.10 m/ s 2

Return to Problem 2

d = (0 m/s)*(2.60 s)+ 0.5*(-9.8 m/s 2 )*(2.60 s) 2

d = -33.1 m (- indicates direction)

v f = v i + a*t

v f = 0 + (-9.8 m/s 2 )*(2.60 s)

v f = -25.5 m/s (- indicates direction)

Return to Problem 3

a = (46.1 m/s - 18.5 m/s)/(2.47 s)

a = 11.2 m/s 2

d = v i *t + 0.5*a*t 2

d = (18.5 m/s)*(2.47 s)+ 0.5*(11.2 m/s 2 )*(2.47 s) 2

d = 45.7 m + 34.1 m

(Note: the d can also be calculated using the equation v f 2 = v i 2 + 2*a*d)

Return to Problem 4

-1.40 m = (0 m/s)*(t)+ 0.5*(-1.67 m/s 2 )*(t) 2

-1.40 m = 0+ (-0.835 m/s 2 )*(t) 2

(-1.40 m)/(-0.835 m/s 2 ) = t 2

1.68 s 2 = t 2

Return to Problem 5

a = (444 m/s - 0 m/s)/(1.83 s)

a = 243 m/s 2

d = (0 m/s)*(1.83 s)+ 0.5*(243 m/s 2 )*(1.83 s) 2

d = 0 m + 406 m

Return to Problem 6

(7.10 m/s) 2 = (0 m/s) 2 + 2*(a)*(35.4 m)

50.4 m 2 /s 2 = (0 m/s) 2 + (70.8 m)*a

(50.4 m 2 /s 2 )/(70.8 m) = a

a = 0.712 m/s 2

Return to Problem 7

(65 m/s) 2 = (0 m/s) 2 + 2*(3 m/s 2 )*d

4225 m 2 /s 2 = (0 m/s) 2 + (6 m/s 2 )*d

(4225 m 2 /s 2 )/(6 m/s 2 ) = d

Return to Problem 8

d = (22.4 m/s + 0 m/s)/2 *2.55 s

d = (11.2 m/s)*2.55 s

Return to Problem 9

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(2.62 m)

0 m 2 /s 2 = v i 2 - 51.35 m 2 /s 2

51.35 m 2 /s 2 = v i 2

v i = 7.17 m/s

Return to Problem 10

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(1.29 m)

0 m 2 /s 2 = v i 2 - 25.28 m 2 /s 2

25.28 m 2 /s 2 = v i 2

v i = 5.03 m/s

To find hang time, find the time to the peak and then double it.

0 m/s = 5.03 m/s + (-9.8 m/s 2 )*t up

-5.03 m/s = (-9.8 m/s 2 )*t up

(-5.03 m/s)/(-9.8 m/s 2 ) = t up

t up = 0.513 s

hang time = 1.03 s

Return to Problem 11

(521 m/s) 2 = (0 m/s) 2 + 2*(a)*(0.840 m)

271441 m 2 /s 2 = (0 m/s) 2 + (1.68 m)*a

(271441 m 2 /s 2 )/(1.68 m) = a

a = 1.62*10 5 m /s 2

Return to Problem 12

• (NOTE: the time required to move to the peak of the trajectory is one-half the total hang time - 3.125 s.)

First use:  v f  = v i  + a*t

0 m/s = v i  + (-9.8  m/s 2 )*(3.13 s)

0 m/s = v i  - 30.7 m/s

v i  = 30.7 m/s  (30.674 m/s)

Now use:  v f 2  = v i 2  + 2*a*d

(0 m/s) 2  = (30.7 m/s) 2  + 2*(-9.8  m/s 2 )*(d)

0 m 2 /s 2  = (940 m 2 /s 2 ) + (-19.6  m/s 2 )*d

-940  m 2 /s 2  = (-19.6  m/s 2 )*d

(-940  m 2 /s 2 )/(-19.6  m/s 2 ) = d

Return to Problem 13

-370 m = (0 m/s)*(t)+ 0.5*(-9.8 m/s 2 )*(t) 2

-370 m = 0+ (-4.9 m/s 2 )*(t) 2

(-370 m)/(-4.9 m/s 2 ) = t 2

75.5 s 2 = t 2

Return to Problem 14

(0 m/s) 2 = (367 m/s) 2 + 2*(a)*(0.0621 m)

0 m 2 /s 2 = (134689 m 2 /s 2 ) + (0.1242 m)*a

-134689 m 2 /s 2 = (0.1242 m)*a

(-134689 m 2 /s 2 )/(0.1242 m) = a

a = -1.08*10 6 m /s 2

(The - sign indicates that the bullet slowed down.)

Return to Problem 15

d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s 2 )*(3.41 s) 2

d = 0 m+ 0.5*(-9.8 m/s 2 )*(11.63 s 2 )

d = -57.0 m

(NOTE: the - sign indicates direction)

Return to Problem 16

(0 m/s) 2 = v i 2 + 2*(- 3.90 m/s 2 )*(290 m)

0 m 2 /s 2 = v i 2 - 2262 m 2 /s 2

2262 m 2 /s 2 = v i 2

v i = 47.6 m /s

Return to Problem 17

( 88.3 m/s) 2 = (0 m/s) 2 + 2*(a)*(1365 m)

7797 m 2 /s 2 = (0 m 2 /s 2 ) + (2730 m)*a

7797 m 2 /s 2 = (2730 m)*a

(7797 m 2 /s 2 )/(2730 m) = a

a = 2.86 m/s 2

88.3 m/s = 0 m/s + (2.86 m/s 2 )*t

(88.3 m/s)/(2.86 m/s 2 ) = t

t = 30. 8 s

Return to Problem 18

( 112 m/s) 2 = (0 m/s) 2 + 2*(a)*(398 m)

12544 m 2 /s 2 = 0 m 2 /s 2 + (796 m)*a

12544 m 2 /s 2 = (796 m)*a

(12544 m 2 /s 2 )/(796 m) = a

a = 15.8 m/s 2

Return to Problem 19

v f 2 = v i 2 + 2*a*d

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(91.5 m)

0 m 2 /s 2 = v i 2 - 1793 m 2 /s 2

1793 m 2 /s 2 = v i 2

v i = 42.3 m/s

Now convert from m/s to mi/hr:

v i = 42.3 m/s * (2.23 mi/hr)/(1 m/s)

v i = 94.4 mi/hr

Return to Problem 20

Physics Problems with Solutions

• Electric Circuits
• Electrostatic
• Calculators
• Practice Tests
• Simulations

Motion Problems, Questions with Solutions and Tutorials

Free questions and problems related to the SAT test and tutorials on rectilinear motion with either uniform velocity or uniform acceleration are included. The concepts of displacement, distance, velocity, speed, acceleration are thoroughly discussed. Problems, questions and examples are presented with solutions and detailed explanations. Graphical analysis of motion problems are also included.

Projectile Equations, Problems and Solutions

• Projectile Problems with Solutions and Explanations
• Solutions and Explanations to Projectile Problems
• Projectile Equations with Explanations

Distance and Displacement

• Displacement and Distance: Tutorials with Examples
• Displacement and Distance: Problems with Solutions

Velocity and Speed

• Velocity and Speed: Tutorials with Examples
• Velocity and Speed: Problems with Solutions

Uniform Acceleration

• Acceleration: Tutorials with Examples
• Uniform Acceleration Motion: Problems with Solutions
• Uniform Acceleration Motion: Equations with Explanations

Graphical Analysis of Motion

• Free SAT II Physics Practice Questions with Solutions on Graphical Analysis of Motion with detailed solutions

Formulas and Constants

• Physics Formulas Reference
• SI Prefixes Used with Units in Physics, Chemistry and Engineering
• Constants in Physics, Chemistry and Engineering

POPULAR PAGES

privacy policy

• C++ Programming
• Differential Equations
• Linear Algebra
• Mechanics of Materials
• Project Management
• Structural Analysis

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• Science Experiments for Kids
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Example Physics Problems and Solutions

Learning how to solve physics problems is a big part of learning physics. Here’s a collection of example physics problems and solutions to help you tackle problems sets and understand concepts and how to work with formulas:

Physics Homework Tips Physics homework can be challenging! Get tips to help make the task a little easier.

Unit Conversion Examples

There are now too many unit conversion examples to list in this space. This Unit Conversion Examples page is a more comprehensive list of worked example problems.

Newton’s Equations of Motion Example Problems

Equations of Motion – Constant Acceleration Example This equations of motion example problem consist of a sliding block under constant acceleration. It uses the equations of motion to calculate the position and velocity of a given time and the time and position of a given velocity.

Equations of Motion Example Problem – Constant Acceleration This example problem uses the equations of motion for constant acceleration to find the position, velocity, and acceleration of a breaking vehicle.

Equations of Motion Example Problem – Interception

This example problem uses the equations of motion for constant acceleration to calculate the time needed for one vehicle to intercept another vehicle moving at a constant velocity.

Vertical Motion Example Problem – Coin Toss Here’s an example applying the equations of motion under constant acceleration to determine the maximum height, velocity and time of flight for a coin flipped into a well. This problem could be modified to solve any object tossed vertically or dropped off a tall building or any height. This type of problem is a common equation of motion homework problem.

Projectile Motion Example Problem This example problem shows how to find different variables associated with parabolic projectile motion.

Accelerometer and Inertia Example Problem Accelerometers are devices to measure or detect acceleration by measuring the changes that occur as a system experiences an acceleration. This example problem uses one of the simplest forms of an accelerometer, a weight hanging from a stiff rod or wire. As the system accelerates, the hanging weight is deflected from its rest position. This example derives the relationship between that angle, the acceleration and the acceleration due to gravity. It then calculates the acceleration due to gravity of an unknown planet.

Weight In An Elevator Have you ever wondered why you feel slightly heavier in an elevator when it begins to move up? Or why you feel lighter when the elevator begins to move down? This example problem explains how to find your weight in an accelerating elevator and how to find the acceleration of an elevator using your weight on a scale.

Equilibrium Example Problem This example problem shows how to determine the different forces in a system at equilibrium. The system is a block suspended from a rope attached to two other ropes.

Equilibrium Example Problem – Balance This example problem highlights the basics of finding the forces acting on a system in mechanical equilibrium.

Force of Gravity Example This physics problem and solution shows how to apply Newton’s equation to calculate the gravitational force between the Earth and the Moon.

Coupled Systems Example Problems

Coupled systems are two or more separate systems connected together. The best way to solve these types of problems is to treat each system separately and then find common variables between them. Atwood Machine The Atwood Machine is a coupled system of two weights sharing a connecting string over a pulley. This example problem shows how to find the acceleration of an Atwood system and the tension in the connecting string. Coupled Blocks – Inertia Example This example problem is similar to the Atwood machine except one block is resting on a frictionless surface perpendicular to the other block. This block is hanging over the edge and pulling down on the coupled string. The problem shows how to calculate the acceleration of the blocks and the tension in the connecting string.

Friction Example Problems

These example physics problems explain how to calculate the different coefficients of friction.

Friction Example Problem – Block Resting on a Surface Friction Example Problem – Coefficient of Static Friction Friction Example Problem – Coefficient of Kinetic Friction Friction and Inertia Example Problem

Momentum and Collisions Example Problems

These example problems show how to calculate the momentum of moving masses.

Momentum and Impulse Example Finds the momentum before and after a force acts on a body and determine the impulse of the force.

Elastic Collision Example Shows how to find the velocities of two masses after an elastic collision.

It Can Be Shown – Elastic Collision Math Steps Shows the math to find the equations expressing the final velocities of two masses in terms of their initial velocities.

Simple Pendulum Example Problems

These example problems show how to use the period of a pendulum to find related information.

Find the Period of a Simple Pendulum Find the period if you know the length of a pendulum and the acceleration due to gravity.

Find the Length of a Simple Pendulum Find the length of the pendulum when the period and acceleration due to gravity is known.

Find the Acceleration due to Gravity Using A Pendulum Find ‘g’ on different planets by timing the period of a known pendulum length.

Harmonic Motion and Waves Example Problems

These example problems all involve simple harmonic motion and wave mechanics.

Energy and Wavelength Example This example shows how to determine the energy of a photon of a known wavelength.

Hooke’s Law Example Problem An example problem involving the restoring force of a spring.

Wavelength and Frequency Calculations See how to calculate wavelength if you know frequency and vice versa, for light, sound, or other waves.

Heat and Energy Example Problems

Heat of Fusion Example Problem Two example problems using the heat of fusion to calculate the energy required for a phase change.

Specific Heat Example Problem This is actually 3 similar example problems using the specific heat equation to calculate heat, specific heat, and temperature of a system.

Heat of Vaporization Example Problems Two example problems using or finding the heat of vaporization.

Ice to Steam Example Problem Classic problem melting cold ice to make hot steam. This problem brings all three of the previous example problems into one problem to calculate heat changes over phase changes.

Charge and Coulomb Force Example Problems

Electrical charges generate a coulomb force between themselves proportional to the magnitude of the charges and inversely proportional to the distance between them. Coulomb’s Law Example This example problem shows how to use Coulomb’s Law equation to find the charges necessary to produce a known repulsive force over a set distance. Coulomb Force Example This Coulomb force example shows how to find the number of electrons transferred between two bodies to generate a set amount of force over a short distance.

Gurumuda Networks

Newton’s first law of motion – problems and solutions

1. A person is in an elevator that moving upward at a constant velocity . The weight of the person is 800 N. Immediately the elevator rope is broke, so the elevator falls. Determine the normal force acted by elevator’s floor to the person just before and after the elevator’s rope broke.

A. 800 N and 0

B. 800 N and 800 N

C. 1600 N and 0

D. 1600 N and 800 N

Weight (w) = 800 Newton

Wanted: The normal force (N)

Before the elevator’s rope broke

When the person stands on the floor of the elevator, weight acts on the person where the direction of the person is downward. That person at rest so that there must a normal force acts on the person, where the direction of the normal force is upward and the magnitude of the normal force same as the magnitude of the weight.

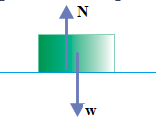
N = 800 Newton

After the elevator’s rope broke

After the elevator’s rope broke, the elevator and the person free fall together, where the magnitude and the direction of their acceleration same as acceleration due to gravity. There is no normal force on the person.

The correct answer is A.

2. A block with a mass of 20 gram moves at a constant velocity on a rough horizontal floor at a constant velocity if there is an external force of 2 N acts on the block. Determine the magnitude of the friction force experienced by the block.

Mass (m) = 20 gram

Force (F) = 2 Newton

Wanted: Magnitude of friction force experienced by the block.

– The magnitude of friction force (F fric ) same as the magnitude of the external force (F)

– The friction force (F fric ) has opposite direction with the external force (F)

Apply Newton’s first law of motion :

F – F fric = 0

F fric = 2 Newton

The correct answer is C.

3. A smooth inclined plane with the length of 0.6 m and height of 0.4 m. A block with the weight of, 1350 N will move upward using the inclined plane. Determine the magnitude of force need to move the block.

Weight of block (w) = 1350 Newton

hyp = 0.6 m

opp = 0.4 m

Wanted : The minimum force

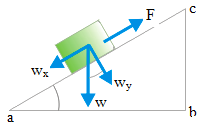
opp = bc = 0.4 m

Sin θ = bc / ac = 0.4 / 0.6 = 4/6 = 2/3

Based on Newton’s first law of motion, the block start to moves upward then the external force (F) minimal same as the horizontal component of weight (w x ).

F – w x = 0

If F = w x , then object start to moving upward at constant velocity.

w x = w sin θ = (1350)(2/3) = (2)(450) = 900 Newton

The correct answer is D.

4. Three forces, F 1 = 22 N, F 2 = 18 N and F 3 = 40 N act on a block. Which figure describes Newton’s first law.

Newton’s first law : Net force (ΣF) = 0.

A. F 1 + F 2 – F 3 = 22 N + 18 N – 40 N = 40 N – 40 N = 0

B. F 2 + F 3 – F 1 = 18 N + 40 N – 22 N = 58 N – 22 N = 36 N (rightward)

C. F 2 + F 3 – F 1 = 18 N + 40 N – 22 N = 58 N – 22 N = 36 N (rightward)

D. F 1 + F 3 – F 2 = 22 N + 40 N – 18 N = 62 N – 18 N = 44 N (leftward)

Share this:

Leave a comment cancel reply.