fraction problem solving questions

Word Problems on Fraction

In word problems on fraction we will solve different types of problems on multiplication of fractional numbers and division of fractional numbers.

I. Word Problems on Addition of Fractions:

1. Nairitee took $\frac{7}{8}$ hour to paint a table and $\frac{2}{3}$ hour to paint a chair. How much time did he take in painting both items?

Total time taken in painting both items = $\frac{7}{8}$ h + $\frac{2}{3}$ h = ($\frac{7}{8}$ + $\frac{2}{3}$) h

= ($\frac{21 + 16}{24}$) h

= $\frac{37}{24}$ h

= 1$\frac{13}{24}$ h

Therefore, Nairitee took 1$\frac{13}{24}$ hours in painting both items.

2. Nitheeya and Nairitee $\frac{3}{10}$ and $\frac{1}{6}$ of a cake respectively. What portion of the cake did they eat together?

The portion of cake ate by Nitheeya = $\frac{3}{10}$

The portion of cake ate by Nitheeya = $\frac{1}{6}$ The portion they ate together = $\frac{3}{10}$ + $\frac{1}{6}$

= $\frac{9}{30}$ + $\frac{5}{30}$; [Since, LCM of 10 and 6 = 30]

= $\frac{9 + 5}{30}$

= $\frac{14}{30}$

= $\frac{7}{15}$

Therefore, together Nitheeya and Nairitee ate $\frac{7}{15}$ of the cake.

3. Rachel took $\frac{1}{2}$ hour to paint a table and $\frac{1}{3}$ hour to paint a chair. How much time did she take in all?

II. Word Problems on Subtraction of Fractions:

1. Out of $\frac{12}{17}$ m of cloth given to a tailor, $\frac{1}{5}$ m were used. Find the length of cloth unused.

Length of the cloth given to the tailors = $\frac{12}{17}$ m

Length of cloth used = $\frac{1}{5}$ m

Length of the unused cloth = $\frac{12}{17}$ m - $\frac{1}{5}$ m

= ($\frac{12}{17}$ - $\frac{1}{5}$) m

= ($\frac{12 × 5}{17 × 5}$ - $\frac{1 × 17}{5 × 17}$) m; [Since, LCM of 17 and 5 = 85]

= ($\frac{60}{85}$ - $\frac{17}{85}$) m

= ($\frac{60 - 17}{85}$ m

= ($\frac{43}{85}$ m

2. Nairitee has $6$\frac{4}{7}$. She gives $4$\frac{2}{3}$ to her mother. How much money does she have now?

Money with Nairitee = $6$\frac{4}{7}$

Money given to her mother = $4$\frac{2}{3}$

Money left with Nairitee = $6$\frac{4}{7}$ - $4$\frac{2}{3}$

= $(6$\frac{4}{7}$ - 4$\frac{2}{3}$)

= $($\frac{46}{7}$ - $\frac{14}{3}$)

= $($\frac{46 × 3}{7 × 3}$ - $\frac{14 × 7}{3 × 7}$) ; [Since, LCM of 7 and 3 = 21]

= $($\frac{138}{21}$ - $\frac{98}{21}$)

= $$\frac{40}{21}$

= $1$\frac{19}{21}$

Therefore, Nairitee has $1$\frac{19}{21}$.

3. If 3$\frac{1}{2}$ m of wire is cut from a piece of 10 m long wire, how much of wire is left?

Total length of the wire = 10 m

Fraction of the wire cut out = 3$\frac{1}{2}$ m = $\frac{7}{2}$ m

Length of the wire left = 10 m – 3$\frac{1}{2}$ m

= [$\frac{10}{1}$ - $\frac{7}{2}$] m, [L.C.M. of 1, 2 is 2]

= [$\frac{20}{2}$ - $\frac{7}{2}$] m, [$\frac{10}{1}$ × $\frac{2}{2}$]

= [$\frac{20 - 7}{2}$] m

= $\frac{13}{2}$ m

= 6$\frac{1}{2}$ m

III. Word Problems on Multiplication of Fractions:

1. $\frac{4}{7}$ of a number is 84. Find the number. Solution: According to the problem, $\frac{4}{7}$ of a number = 84 Number = 84 × $\frac{7}{4}$ [Here we need to multiply 84 by the reciprocal of $\frac{4}{7}$]

$Word Problems on Fraction$

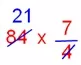
= 21 × 7 = 147 Therefore, the number is 147.

2. One half of the students in a school are girls, $\frac{3}{5}$ of these girls are studying in lower classes. What fraction of girls are studying in lower classes?

Fraction of girls studying in school = $\frac{1}{2}$

Fraction of girls studying in lower classes = $\frac{3}{5}$ of $\frac{1}{2}$

= $\frac{3}{5}$ × $\frac{1}{2}$

= $\frac{3 × 1}{5 × 2}$

= $\frac{3}{10}$

Therefore, $\frac{3}{10}$ of girls studying in lower classes.

3. Maddy reads three-fifth of 75 pages of his lesson. How many more pages he need to complete the lesson? Solution: Maddy reads = $\frac{3}{5}$ of 75 = $\frac{3}{5}$ × 75

$Word Problems on Fraction$

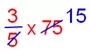
= 45 pages. Maddy has to read = 75 – 45. = 30 pages. Therefore, Maddy has to read 30 more pages.

IV. Word Problems on Division of Fractions:

1. A herd of cows gives 4 litres of milk each day. But each cow gives one-third of total milk each day. They give 24 litres milk in six days. How many cows are there in the herd?

Solution: A herd of cows gives 4 litres of milk each day. Each cow gives one-third of total milk each day = $\frac{1}{3}$ of 4 Therefore, each cow gives $\frac{4}{3}$ of milk each day. Total no. of cows = 4 ÷ $\frac{4}{3}$ = 4 × $\frac{3}{4}$ = 3 Therefore there are 3 cows in the herd.

Worksheet on Word problems on Fractions:

1. Shelly walked $\frac{1}{3}$ km. Kelly walked $\frac{4}{15}$ km. Who walked farther? How much farther did one walk than the other?

2. A frog took three jumps. The first jump was $\frac{2}{3}$ m long, the second was $\frac{5}{6}$ m long and the third was $\frac{1}{3}$ m long. How far did the frog jump in all?

3. A vessel contains 1$\frac{1}{2}$ l of milk. John drinks $\frac{1}{4}$ l of milk; Joe drinks $\frac{1}{2}$ l of milk. How much of milk is left in the vessel?

4. Between 4$\frac{2}{3}$and 3$\frac{2}{3}$ which is greater and by how much?

5. What must be subtracted from 5$\frac{1}{6}$ to get 2$\frac{1}{8}$?

You might like these

$To convert a mixed number into an improper fraction, we multiply the whole number by the denominator of the proper fraction and then to the product add the numerator of the fraction to get the numerator of the improper fraction. I$

Conversion of Mixed Fractions into Improper Fractions |Solved Examples

To convert a mixed number into an improper fraction, we multiply the whole number by the denominator of the proper fraction and then to the product add the numerator of the fraction to get the numerator of the improper fraction. I

$The three types of fractions are : Proper fraction, Improper fraction, Mixed fraction, Proper fraction: Fractions whose numerators are less than the denominators are called proper fractions. (Numerator < denominator). Two parts are shaded in the above diagram.$

Types of Fractions |Proper Fraction |Improper Fraction |Mixed Fraction

The three types of fractions are : Proper fraction, Improper fraction, Mixed fraction, Proper fraction: Fractions whose numerators are less than the denominators are called proper fractions. (Numerator < denominator). Two parts are shaded in the above diagram.

$In 5th Grade Fractions we will discuss about definition of fraction, concept of fractions and different types of examples on fractions. A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.$

5th Grade Fractions | Definition | Examples | Word Problems |Worksheet

In 5th Grade Fractions we will discuss about definition of fraction, concept of fractions and different types of examples on fractions. A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.

$In conversion of improper fractions into mixed fractions, we follow the following steps: Step I: Obtain the improper fraction. Step II: Divide the numerator by the denominator and obtain the quotient and remainder. Step III: Write the mixed fraction$

Conversion of Improper Fractions into Mixed Fractions |Solved Examples

In conversion of improper fractions into mixed fractions, we follow the following steps: Step I: Obtain the improper fraction. Step II: Divide the numerator by the denominator and obtain the quotient and remainder. Step III: Write the mixed fraction

$The fractions having the same value are called equivalent fractions. Their numerator and denominator can be different but, they represent the same part of a whole. We can see the shade portion with respect to the whole shape in the figures from (i) to (viii) In; (i) Shaded$

Equivalent Fractions | Fractions |Reduced to the Lowest Term |Examples

The fractions having the same value are called equivalent fractions. Their numerator and denominator can be different but, they represent the same part of a whole. We can see the shade portion with respect to the whole shape in the figures from (i) to (viii) In; (i) Shaded

$To find the difference between like fractions we subtract the smaller numerator from the greater numerator. In subtraction of fractions having the same denominator, we just need to subtract the numerators of the fractions.$

Subtraction of Fractions having the Same Denominator | Like Fractions

To find the difference between like fractions we subtract the smaller numerator from the greater numerator. In subtraction of fractions having the same denominator, we just need to subtract the numerators of the fractions.

$Any two like fractions can be compared by comparing their numerators. The fraction with larger numerator is greater than the fraction with smaller numerator, for example $\frac{7}{13}$ > $\frac{2}{13}$ because 7 > 2. In comparison of like fractions here are some$

Comparison of Like Fractions | Comparing Fractions | Like Fractions

Any two like fractions can be compared by comparing their numerators. The fraction with larger numerator is greater than the fraction with smaller numerator, for example $\frac{7}{13}$ > $\frac{2}{13}$ because 7 > 2. In comparison of like fractions here are some

$In comparison of fractions having the same numerator the following rectangular figures having the same lengths are divided in different parts to show different denominators. 3/10 < 3/5 < 3/4 or 3/4 > 3/5 > 3/10 In the fractions having the same numerator, that fraction is$

Comparison of Fractions having the same Numerator|Ordering of Fraction

In comparison of fractions having the same numerator the following rectangular figures having the same lengths are divided in different parts to show different denominators. 3/10 3/5 > 3/10 In the fractions having the same numerator, that fraction is

$In worksheet on comparison of like fractions, all grade students can practice the questions on comparison of like fractions. This exercise sheet on comparison of like fractions can be practiced$

Worksheet on Comparison of Like Fractions | Greater & Smaller Fraction

In worksheet on comparison of like fractions, all grade students can practice the questions on comparison of like fractions. This exercise sheet on comparison of like fractions can be practiced

$Like and unlike fractions are the two groups of fractions: (i) 1/5, 3/5, 2/5, 4/5, 6/5 (ii) 3/4, 5/6, 1/3, 4/7, 9/9 In group (i) the denominator of each fraction is 5, i.e., the denominators of the fractions are equal. The fractions with the same denominators are called$

Like and Unlike Fractions | Like Fractions |Unlike Fractions |Examples

Like and unlike fractions are the two groups of fractions: (i) 1/5, 3/5, 2/5, 4/5, 6/5 (ii) 3/4, 5/6, 1/3, 4/7, 9/9 In group (i) the denominator of each fraction is 5, i.e., the denominators of the fractions are equal. The fractions with the same denominators are called

● Multiplication is Repeated Addition.

● Multiplication of Fractional Number by a Whole Number.

● Multiplication of a Fraction by Fraction.

● Properties of Multiplication of Fractional Numbers.

● Multiplicative Inverse.

● Worksheet on Multiplication on Fraction.

● Division of a Fraction by a Whole Number.

● Division of a Fractional Number.

● Division of a Whole Number by a Fraction.

● Properties of Fractional Division.

● Worksheet on Division of Fractions.

● Simplification of Fractions.