experiment in math meaning

Something that can be repeated that has a set of possible results.

Examples: • Rolling dice to see what random numbers come up. • Asking your friends to choose a favorite pet from a list

Experiments help us find out information by collecting data in a careful manner.

In probability and statistics, an experiment typically refers to a study in which the experimenter is trying to determine whether there is a relationship between two or more variables. In an experiment, the subjects are randomly assigned to either a treatment group or a control group (there can be more than one of either group).

Generally, the control group in an experiment receives a placebo (substance that has no effect) or no treatment at all. The treatment group receives the experimental treatment. The goal of the experiment is to determine whether or not the treatment has the desired/any effect that differs from the control group to a degree that the difference can be attributed to the treatment rather than to random chance or variability. Well-designed experiments can yield informative and unambiguous conclusions about cause and effect relationships.

As an example, if a scientist wants to test whether a new medication they developed has any effect, they would select subjects from a common population and randomly assign them to either a treatment group or a control group. They would then administer the treatment to the treatment group, and either a placebo or no treatment to the control group, and study the effects of each using statistical measures to determine whether the medication had any effect beyond chance or variability.

Note that an experiment does not necessarily need to have a physical treatment. The term "treatment" is used fairly loosely. Another experiment could look at the effects of getting advice from a college counselor on admission rates compared to not getting advice from a college counselor. In this case, the "treatment" would be getting advice from a college counselor. The control group would get no advice from a college counselor.

Importance of experimental design

Like survey methodology , experimental design is essential to the validity of the results of the experiment. A poorly designed experiment can result in false or incorrect conclusions. Proper statistical experiment design generally involves the following:

• Identification of the explanatory variable, also referred to as the independent variable . The explanatory variable is the "treatment," or the thing that causes the change, and can be anything that causes a change in the response variable.
• Identification of the response variable, also referred to as the dependent variable . It is the variable that may be affected by the explanatory/independent variable.
• Defining the population of interest and taking a random sample from the population. Generally the larger the random sample, the less potential for sample error, since the larger sample will likely be more representative of the population.
• Random assignment of the subjects in the sample to either the treatment group or the control group.
• Administration of the treatment to the treatment group, and placebo (or nothing) to the control group), possibly using a blind experiment (the subject doesn't know whether they are receiving the treatment or the placebo) or double blind experiment (neither experimenter nor subject knows which treatment they are getting).
• Measurement of the response over a chosen period of time.
• Statistical analysis of the supposed response to determine whether there is an actual response, or the response can be attributed to chance, to determine whether there is a causal relationship between the treatment and the response.
• Replication of the experiment by peers, assuming there is a causal relationship between the treatment and the response.

Experiments vs surveys

Experiments and surveys are both techniques used as part of inferential statistics . A survey involves the use of a random sample of the population, rather than the whole, with the goal that all subjects in the population have an equal chance of being selected. The random sample of the population is then used to draw conclusions or make inferences about the population as a whole.

In contrast, an experiment typically involves the use of random assignment such that all subjects have an equal chance of being assigned to the groups (treatment and control) in the study, which minimizes potential biases, as well as allows the experimenters to evaluate the role of variability in the experiment. This in turn allows them to determine whether any observed differences between the groups merit further study or not based on whether or not the differences can be attributed to variability or chance.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Experiment | Definition & Meaning

JUMP TO TOPIC

Basics of an Experiment 

Controlled variables, independent variable, dependent variable, types of experiments, experiment|definition & meaning.

An experiment is a series of procedures and results that are carried out to answer a specific issue or problem or to confirm or disprove a theory or body of knowledge about a phenomenon.

Figure 1: Illustration of an Experiment

The scientific method, a methodical approach to learning about the world around you, is founded on the concept of the experiment . Even while some experiments are conducted in labs, you can conduct an experiment at every time and everywhere.

• The key stages of the scientific process are as follows:
• Keenly Observe things.
• Develop a hypothesis .
• Create and carry out an experiment to verify Your hypothesis.
• Analyze the findings of your experiment.
• Based on the analysis of your results, approve or refute your hypothesis.
• Create a new hypothesis , if required, and evaluate it.

Types of Variables in an Experiment

A variable is, to put it simply, everything that can be altered or managed throughout an experiment. Humidity, the length of the study, the structure of an element, the intensity of sunlight, etc. are typical examples of variables. In any study, there are 3 major types of variables :

• Controlled variables (c.v)
• Independent variables (i.v)
• Dependent variables (d.v).

Figure 2: Illustration of Types of Variables

Variables that are maintained constant or unchangeable are known as controlled variables, sometimes known as constant variables. For instance, if you were evaluating the amount of fizz emitted by various sodas, you may regulate the bottle size to ensure that all soda manufacturers were in 12- ounce bottles. If you were conducting an experiment on the effects of spraying plants with various chemicals, you will attempt to keep a similar pressure and perhaps a similar amount when spraying the plants.

The only variable that  you can modify  is the independent variable. It is one factor as you typically try to adjust one element at a time in experiments. As a result, measuring and interpretation of data are made quite simple. For instance, if you’re attempting to establish whether raising the temperature makes it possible to solvate more amount of sugar in the water, the water temperature is the independent variable. This is the factor that you are consciously in control of.

The variable that is  monitored  to determine whether or not your independent variable has an impact is known as the dependent variable. For instance, in the case where you raise the water temperature to observe if it has an impact on the solubility of sugar in it, the weight or volume of sugar (depending on which one you want to calculate) will be the dependent variable.

There are three main types of experiments. Each has its own pros and cons and is carried out according to the nature of the given scenario and desired outcomes. Following are the names of these three types.

Quasi Experiment

Controlled experiment, field experiment.

Figure 3: Illustration of Types of Experiments

Each of these experiments is discussed below along with their strengths and weaknesses.

These are often conducted in a natural environment and involve measuring the impact of one object on another to determine its impact (D.V.). In Quasi-experiments, the research is simply assessing the impact of an event that is already occurring because there is no intentional modification of the variable in this instance; rather, it is changing naturally.

Owing to the unavailability of the researcher, variables occur   naturally , allowing for easy generalization of results to other (real-life) situations, which leads to greater ecological validity.

Absence of control – Quasi-experiments possess poor internal validity since the experimenter cannot always precisely analyze the impact of the independent variable because there is no influence over the environment or other supplementary variables.

Non-repeatable – Because the researcher has no control over the research process, the validity of the findings cannot be verified.

Controlled experiments are also known as lab experiments . Controlled experiments are carried out under carefully monitored conditions, with the researcher purposefully altering one variable (Independent Variable) to determine how it affects another (dependent Variable).

Control – lab studies have a higher level of environmental and other extrinsic variable control, which allows the scientist to precisely examine the impact of the Independent Variable, increasing internal validity.

Replicable – because of the researcher’s greater degree of control, research techniques may be replicated so that the accuracy of the findings can be verified.

Absence of ecological validity — results are difficult to generalize to other (real-life) situations because of the researcher’s participation in modifying and regulating variables, which leads to poor external validity.

A field experiment could be a controlled or a Quasi-experiment. Instead of taking place in a laboratory, it occurs in the actual world. An illustration of a field experiment could be one that involved an organism in its natural environment.

Validity : Because field experiments are carried out in a natural setting and with a certain level of control, they are considered to possess adequate internal and external validity.

Internal validity is believed to be poorer because there is less control than in lab trials, making it more probable that uncontrollable factors would skew results.

An Example of Identifying the Variables in an Experiment

A farmer wants to determine the effect of different amounts of fertilizer on his crop yield. The farmer does not change the amount of water given to the crop for different amounts of fertilizer applied to the field. Determine which of the variables is the controlled variable, independent variable, and independent variable. Also, mention the reasons behind it.

Figure 4: Illustration of the Example

Controlled variable : The amount of water given to the crop is a controlled variable since it is not changed when different amounts of fertilizer are applied.

Independent variable : The amount of fertilizer added to crops is the independent variable. This is because it is the variable which is being manipulated to determine its impact on crop yield.

Dependent variable : Crop yield is the dependent variable in this example. This is because it is the variable on which the impact of the independent variable (Amount of fertilizer) is being monitored .

All images/mathematical drawings were created with GeoGebra.

Event Definition < Glossary Index > Exponent Definition

Experimental Probability

Experimental probability: introduction, experimental probability: definition, experimental probability formula, solved examples, practice problems, frequently asked questions.

In mathematics, probability refers to the chance of occurrence of a specific event. Probability can be measured on a scale from 0 to 1. The probability is 0 for an impossible event. The probability is 1 if the occurrence of the event is certain.

There are two approaches to study probability: experimental and theoretical. 

Suppose you and your friend toss a coin to decide who gets the first turn to ride a new bicycle. You choose “heads” and your friend chooses “tails.” 

Can you guess who will win? No! You have $\frac{1}{2}$ a chance of winning and so does your friend. This is theoretical since you are predicting the outcome based on what is expected to happen and not on the basis of outcomes of an experiment.

So, what is the experimental probability? Experimental probability is calculated by repeating an experiment and observing the outcomes. Let’s understand this a little better.

Recommended Games

Experimental probability, or empirical probability, is the probability calculated by performing actual experiments and gathering or recording the necessary information. How would you define an experiment? The math definition of an experiment is “a process or procedure that can be repeated and that has a set of well-defined possible results or outcomes.”

Consider the same example. Suppose you flip the coin 50 times to see whether you get heads or tails, and you record the outcomes. Suppose you get heads 20 times and tails 30 times. Then the probability calculated using these outcomes is experimental probability. Here, t he experimental meaning is connected with such experiments used to determine the probability of an event.

Now that you know the meaning of experimental probability, let’s understand its formula.

Experimental Probability for an Event A can be calculated as follows:

P(E) $= \frac{Number of occurance of the event A}{Total number of trials}$

Let’s understand this with the help of the last example. 

A coin is flipped a total of 50 times. Heads appeared 20 times. Now, what is the experimental probability of getting heads?

E xperimental probability of getting heads $= \frac{Number of occurrences}{Total number of trials}$

P (Heads) $= \frac{20}{50} = \frac{2}{5}$

P (Tails) $= \frac{30}{50} = \frac{3}{5}$

Experimental Probability vs. Theoretical Probability

Theoretical probability expresses what is expected. On the other hand, experimental probability explains how frequently an event occurred in an experiment.

If you roll a die, the theoretical probability of getting any particular number, say 3, is $\frac{1}{6}$. 

However, if you roll the die 100 times and record how many times 3 appears on top, say 65 times, then the experimental probability of getting 3 is $\frac{65}{100}$.

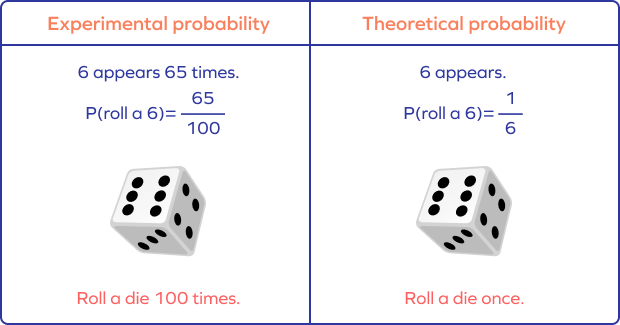
Theoretical probability for Event A can be calculated as follows:

P(A) $= \frac{Number of outcomes favorable to Event A}{Number of possible outcomes}$

In the example of flipping a coin, the theoretical probability of the occurrence of heads (or tails) on tossing a coin is

P(H) $= \frac{1}{2}$ and  P(T) $= \frac{1}{2}$ (since possible outcomes are $2 -$ head or tail)

Experimental Probability: Examples

Let’s take a look at some of the examples of experimental probability .

Example 1: Ben tried to toss a ping-pong ball in a cup using 10 trials, out of which he succeeded 4 times. 

P(win) $= \frac{Number of success}{Number of trials}$

             $= \frac{4}{10}$

             $= \frac{2}{5}$

Example 2: Two students are playing a game of die. They want to know how many times they land on 2 on the dice if the die is rolled 20 times in a row. 

The experimental probability of rolling a 2 

$= \frac{Number of times 2 appeared}{Number of trials}$

$= \frac{5}{20}$

$= \frac{1}{4}$

1. Probability of an event always lies between 0 and 1.

2. You can also express the probability as a decimal and a percentage.

Experimental probability is a probability that is determined by the results of a series of experiments. Learn more such interesting concepts at SplashLearn .

1. Leo tosses a coin 25 times and observes that the “head” appears 10 times. What is the experimental probability of getting a head?

 P(Head) $= \frac{Number of times heads appeared}{Total number of trials}$

               $= \frac{10}{25}$

               $= \frac{2}{5}$

               $= 0.4$

2. The number of cakes a baker makes per day in a week is given as 7, 8, 6, 10, 2, 8, 3. What is the probability that the baker makes less than 6 cakes the next day?

Solution: 

Number of cakes baked each day in a week $= 7, 8, 6, 10, 2, 8, 3$

Out of 7 days, there were 2 days (highlighted in bold) on which the baker made less than 6 cookies.

P$(< 6 $cookies$) = \frac{2}{7}$

3. The chart below shows the number of times a number was shown on the face of a tossed die. What was the probability of getting a 3 in this experiment?

Number of times 3 showed $= 7$

Number of tosses $= 30$

P(3) $= \frac{7}{30}$

4. John kicked a ball 20 times. He kicked 16 field goals and missed 4 times . What is the experimental probability that John will kick a field goal during the game?

Solution:  

John succeeded in kicking 16 field goals. He attempted to kick a field goal 20 times. 

So, the number of trials $= 20$

John’s experimental probability of kicking a field goal $= \frac{Successful outcomes} {Trials attempted} = \frac{16}{20}$ 

$= \frac{4}{5}$

$= 0.8$ or $80%$

5. James recorded the color of bikes crossing his street. Of the 500 bikes, 10 were custom colors, 100 were white, 50 were red, 120 were black, 100 were silver, 60 were blue, and 60 were gray. What is the probability that the car crossing his street is white?

Number of white bikes $= 100$ 

Total number of bikes $= 500$

P(white bike) $=  \frac{100}{500} = \frac{1}{5}$

Attend this quiz & Test your knowledge.

In a class, a student is chosen randomly in five trials to participate in 5 different events. Out of chosen students, 3 were girls and 2 were boys. What is the experimental probability of choosing a boy in the next event?

A manufacturer makes 1000 tablets every month. after inspecting 100 tablets, the manufacturer found that 30 tablets were defective. what is the probability that you will buy a defective tablet, the 3 coins are tossed 1000 times simultaneously and we get three tails $= 160$, two tails $= 260$, one tail $= 320$, no tails $= 260$. what is the probability of occurrence of two tails, the table below shows the colors of shirts sold in a clothing store on a particular day and their respective frequencies. use the table to answer the questions that follow. what is the probability of selling a blue shirt.

Jason leaves for work at the same time each day. Over a period of 327 working days, on his way to work, he had to wait for a train at the railway crossing for 68 days. What is the experimental probability that Jason has to wait for a train on his way to work?

What is the importance of experimental probability?

Experimental probability is widely used in research and experiments in various fields, such as medicine, social sciences, investing, and weather forecasting.

Is experimental probability always accurate?

Predictions based on experimental probability are less reliable than those based on theoretical probability.

Can experimental probability change every time the experiment is performed?

Since the experimental probability is based on the actual results of an experiment, it can change when the results of an experiment change.

What is theoretical probability?

The theoretical probability is calculated by finding the ratio of the number of favorable outcomes to the total number of probable outcomes.

RELATED POSTS

• Length Conversion – Metric and Customary System, Examples
• How Many Weeks Are There in a Month? Definition with Examples
• Analog Clock – Definition, Clock Face, Clock Hands, Examples, Facts
• Slope of Parallel Line: Formula, Derivation, Example
• Milliliter – Definition with Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11th Grade Math
• 12th Grade Math
• Trigonometry
• Physics Tutoring
• Guitar Lessons
• Piano Lessons
• Foreign Languages
• Study Skills
• ADHD & Learning Disabilities
• Summer Tutoring
• College Planning
• School Support
• SAT and ACT Online
• Own a Franchise

Experiment: Definitions and Examples

Experiment: Definitions, Formulas, & Examples

GET TUTORING NEAR ME!

By submitting the following form, you agree to Club Z!'s Terms of Use and Privacy Policy

Introduction

Experiments are a fundamental part of mathematics, used to test hypotheses and establish relationships between variables. They are used in many fields, including physics, chemistry, biology, psychology, and economics. In this article, we will explore the basics of experiments in math, including definitions, examples, and a quiz to test your understanding.

Definitions

Before we dive into examples, let’s define some key terms related to experiments in math.

• Experiment: A process used to test a hypothesis or investigate a phenomenon. The process involves manipulating one or more variables and measuring the effect on one or more outcomes.
• Hypothesis: A statement or assumption about a phenomenon that is being tested in an experiment.
• Independent variable: The variable that is being manipulated in an experiment. It is also called the predictor variable or the input variable.
• Dependent variable: The variable that is being measured in an experiment. It is also called the response variable or the output variable.
• Control group: A group in an experiment that does not receive the treatment being tested. It is used as a baseline for comparison with the experimental group.
• Experimental group: A group in an experiment that receives the treatment being tested.
• Randomization: The process of randomly assigning subjects to groups in an experiment. This is done to minimize the effect of confounding variables.

Now that we have defined some key terms, let’s explore some examples of experiments in math.

• A scientist wants to test the effect of caffeine on reaction time. She recruits 100 subjects and randomly assigns them to two groups: one group receives caffeine, and the other group receives a placebo. She then measures their reaction time using a computer-based test.
• A researcher wants to test the effect of a new drug on blood pressure. He recruits 200 subjects and randomly assigns them to two groups: one group receives the new drug, and the other group receives a placebo. He then measures their blood pressure at various time points.
• A teacher wants to test the effect of a new teaching method on student performance. She randomly assigns 50 students to two groups: one group receives the new teaching method, and the other group receives the traditional teaching method. She then measures their performance on a standardized test.
• A psychologist wants to test the effect of music on mood. He recruits 30 subjects and randomly assigns them to two groups: one group listens to classical music, and the other group listens to no music. He then measures their mood using a standardized questionnaire.
• An economist wants to test the effect of a tax cut on consumer spending. He collects data on 100 households and measures their spending before and after the tax cut.
• A physicist wants to test the effect of temperature on the viscosity of a liquid. She heats the liquid to different temperatures and measures its viscosity using a viscometer.
• A biologist wants to test the effect of light on plant growth. She grows plants under different light conditions and measures their height and weight after a specified time.
• A mathematician wants to test the effect of an online tutorial on student understanding of a concept. She randomly assigns 50 students to two groups: one group watches the tutorial, and the other group does not. She then measures their understanding using a standardized test.
• A sociologist wants to test the effect of social media on self-esteem. She recruits 100 subjects and randomly assigns them to two groups: one group uses social media for an hour each day, and the other group does not. She then measures their self-esteem using a standardized questionnaire.
• An engineer wants to test the effect of a new manufacturing process on product quality. He randomly assigns 50 products to two groups: one group is manufactured using the new process, and the other group is manufactured using the traditional process. He then measures their quality using a standardized metric.
• What is the purpose of an experiment in math?

The purpose of an experiment in math is to test a hypothesis or investigate a phenomenon by manipulating one or more variables and measuring the effect on one or more outcomes.

• What is the difference between an independent variable and a dependent variable?

The independent variable is the variable that is being manipulated in an experiment, while the dependent variable is the variable that is being measured in the experiment.

• Why is randomization important in experiments?

Randomization is important in experiments because it minimizes the effect of confounding variables and ensures that the groups being compared are as similar as possible, except for the variable being tested.

• What is a control group?

A control group is a group in an experiment that does not receive the treatment being tested. It is used as a baseline for comparison with the experimental group.

• What is a hypothesis?

A hypothesis is a statement or assumption about a phenomenon that is being tested in an experiment.

• What is the purpose of an experiment in math? A) To test a hypothesis or investigate a phenomenon B) To prove a theory C) To collect data randomly D) None of the above
• What is the difference between an independent variable and a dependent variable? A) The independent variable is the variable being measured, and the dependent variable is the variable being manipulated. B) The independent variable is the variable being manipulated, and the dependent variable is the variable being measured. C) There is no difference between the two. D) Both variables are manipulated.
• Why is randomization important in experiments? A) It ensures that the groups being compared are as similar as possible, except for the variable being tested. B) It ensures that the groups being compared are different in every possible way. C) It has no effect on the outcome of the experiment. D) Both A and B.
• What is a control group? A) A group in an experiment that receives the treatment being tested. B) A group in an experiment that does not receive the treatment being tested. C) A group in an experiment that is randomly assigned to a treatment or no-treatment condition. D) Both A and C.
• What is a hypothesis? A) A statement or assumption about a phenomenon that is being tested in an experiment. B) A group in an experiment that receives the treatment being tested. C) A variable being manipulated in an experiment. D) A variable being measured in an experiment.
• A scientist wants to test the effect of exercise on heart rate. She recruits 50 subjects and randomly assigns them to two groups: one group exercises for 30 minutes, and the other group does not. She then measures their heart rate. What is the independent variable? A) Heart rate B) Group assignment (exercise or no exercise) C) Time D) None of the above
• What is the dependent variable in the experiment described in question 6? A) Heart rate B) Group assignment (exercise or no exercise) C) Time D) None of the above
• What is the purpose of a control group? A) To provide a baseline for comparison with the experimental group. B) To manipulate the independent variable. C) To measure the dependent variable. D) Both B and C.
• A researcher wants to test the effect of a new drug on blood sugar levels. He recruits 100 subjects and randomly assigns them to two groups: one group receives the new drug, and the other group receives a placebo. He then measures their blood sugar levels. What is the experimental group in this experiment?
• A researcher wants to test the effect of a new drug on blood sugar levels. He recruits 100 subjects and randomly assigns them to two groups: one group receives the new drug, and the other group receives a placebo. He then measures their blood sugar levels. What is the experimental group in this experiment? A) The group that receives the new drug B) The group that receives the placebo C) Both groups D) Neither group

If you’re interested in online or in-person tutoring on this subject, please contact us and we would be happy to assist!

Experiment:

We guarantee you’ll find the right tutor, or we’ll cover the first hour of your lesson.

Testimonials

Club Z! has connected me with a tutor through their online platform! This was exactly the one-on-one attention I needed for my math exam. I was very pleased with the sessions and ClubZ’s online tutoring interface.

My son was suffering from low confidence in his educational abilities. I was in need of help and quick. Club Z! assigned Charlotte (our tutor) and we love her! My son’s grades went from D’s to A’s and B’s.

I’ve been using Club Z’s online classrooms to receive some help and tutoring for 2 of my college classes. I must say that I am very impressed by the functionality and ease of use of their online App. Working online with my tutor has been a piece of cake. Thanks Z.

Jonathan is doing really well in all of his classes this semester, 5 A’s & 2 B’s (he has a computer essentials class instead of PLC). In his Algebra class that Nathan is helping him with he has an A+.

Sarah is very positive, enthusiastic and encourages my daughter to do better each time she comes. My daughter’s grade has improved, we are very grateful for Sarah and that she is tutoring our daughter. Way to go ClubZ!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.5: Experiments

• Last updated
• Save as PDF
• Page ID 59974

• Darlene Diaz
• Santiago Canyon College via ASCCC Open Educational Resources Initiative

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

So far, we have primarily discussed observational studies – studies in which conclusions would be drawn from observations of a sample or the population. In some cases, these observations might be unsolicited, such as studying the percentage of cars that turn right at a red light even when there is a “no turn on red” sign. In other cases, the observations are solicited, like in a survey or a poll.

In contrast, it is common to use experiments when exploring how subjects react to an outside influence. In an experiment, some kind of treatment is applied to the subjects and the results are measured and recorded.

Definition: Observational Studies and Experiments

An observational study is a study based on observations or measurements.

An experiment is a study in which the effects of a treatment are measured.

Here are some examples of experiments:

Example \(\PageIndex{1}\)

a. A pharmaceutical company tests a new medicine for treating Alzheimer’s disease by administering the drug to 50 elderly patients with recent diagnoses. The treatment here is the new drug.

b. A gym tests out a new weight loss program by enlisting 30 volunteers to try out the program. The treatment here is the new program.

c. You test a new kitchen cleaner by buying a bottle and cleaning your kitchen. The new cleaner is the treatment.

d. A psychology researcher explores the effect of music on temperament by measuring people’s temperament while listening to different types of music. The music is the treatment.

Try It Now 6

Is each scenario describing an observational study or an experiment?

a. The weights of 30 randomly selected people are measured

b. Subjects are asked to do 20 jumping jacks, and then their heart rates are measured

c. Twenty coffee drinkers and twenty tea drinkers are given a concentration test

When conducting experiments, it is essential to isolate the treatment being tested.

Example \(\PageIndex{2}\)

Suppose a middle school (junior high) finds that their students are not scoring well on the state’s standardized math test. They decide to run an experiment to see if an alternate curriculum would improve scores. To run the test, they hire a math specialist to come in and teach a class using the new curriculum. To their delight, they see an improvement in test scores.

The difficulty with this scenario is that it is not clear whether the curriculum is responsible for the improvement, or whether the improvement is due to a math specialist teaching the class. This is called confounding – when it is not clear which factor or factors caused the observed effect. Confounding is the downfall of many experiments, though sometimes it is hidden.

Definition: Confounding

Confounding occurs when there are two potential variables that could have caused the outcome and it is not possible to determine which actually caused the result.

Example \(\PageIndex{3}\)

A drug company study about a weight loss pill might report that people lost an average of 8 pounds while using their new drug. However, in the fine print you find a statement saying that participants were encouraged to also diet and exercise. It is not clear in this case whether the weight loss is due to the pill, to diet and exercise, or a combination of both. In this case confounding has occurred.

Example \(\PageIndex{4}\)

Researchers conduct an experiment to determine whether students will perform better on an arithmetic test if they listen to music during the test. They first give the student a test without music, then give a similar test while the student listens to music. In this case, the student might perform better on the second test, regardless of the music, simply because it was the second test and they were warmed up.

There are a number of measures that can be introduced to help reduce the likelihood of confounding. The primary measure is to use a control group .

Definition: Control Group

When using a control group, the participants are divided into two or more groups, typically a control group and a treatment group. The treatment group receives the treatment being tested; the control group does not receive the treatment.

Ideally, the groups are otherwise as similar as possible, isolating the treatment as the only potential source of difference between the groups. For this reason, the method of dividing groups is important. Some researchers attempt to ensure that the groups have similar characteristics (same number of females, same number of people over 50, etc.), but it is nearly impossible to control for every characteristic. Because of this, random assignment is very commonly used.

Example \(\PageIndex{5}\)

To determine if a two-day prep course would help high school students improve their scores on the SAT test, a group of students was randomly divided into two subgroups. The first group, the treatment group, was given a two-day prep course. The second group, the control group, was not given the prep course. Afterwards, both groups were given the SAT.

Example \(\PageIndex{6}\)

A company testing a new plant food grows two crops of plants in adjacent fields, the treatment group receiving the new plant food and the control group not. The crop yield would then be compared. By growing them at the same time in adjacent fields, they are controlling for weather and other confounding factors.

Sometimes not giving the control group anything does not completely control for confounding variables. For example, suppose a medicine study is testing a new headache pill by giving the treatment group the pill and the control group nothing. If the treatment group showed improvement, we would not know whether it was due to the medicine in the pill, or a response to have taken any pill. This is called a placebo effect .

Definition: Placebo Effect

The placebo effect is when the effectiveness of a treatment is influenced by the patient’s perception of how effective they think the treatment will be, so a result might be seen even if the treatment is ineffectual.

Example \(\PageIndex{7}\)

A study found that when doing painful dental tooth extractions, patients told they were receiving a strong painkiller while actually receiving a saltwater injection found as much pain relief as patients receiving a dose of morphine [ 3 ].

To control the placebo effect, a placebo , or dummy treatment, is often given to the control group. This way, both groups are truly identical except for the specific treatment given.

Definition: Placebo and Placebo Controlled Experiments

A placebo is a dummy treatment given to control for the placebo effect.

An experiment that gives the control group a placebo is called a placebo-controlled experiment .

In some cases, it is more appropriate to compare to a conventional treatment than a placebo. For example, in a cancer research study, it would not be ethical to deny any treatment to the control group or to give a placebo treatment. In this case, the currently acceptable medicine would be given to the second group, called a comparison group in this case. In our SAT test example, the non-treatment group would most likely be encouraged to study on their own, rather than be asked to not study at all, to provide a meaningful comparison.

When using a placebo, it would defeat the purpose if the participant knew they were receiving the placebo.

Definition: Blind Studies

A blind study is one in which the participant does not know whether or not they are receiving the treatment or a placebo.

A double-blind study is one in which those interacting with the participants don’t know who is in the treatment group and who is in the control group.

Example \(\PageIndex{8}\)

In a study about anti-depression medicine, you would not want the psychological evaluator to know whether the patient is in the treatment or control group either, as it might influence their evaluation, so the experiment should be conducted as a double-blind study.

It should be noted that not every experiment needs a control group.

Example \(\PageIndex{9}\)

If a researcher is testing whether a new fabric can withstand fire, she simply needs to torch multiple samples of the fabric – there is no need for a control group.

Try It Now 7

To test a new lie detector, two groups of subjects are given the new test. One group is asked to answer all the questions truthfully, and the second group is asked to lie on one set of questions. The person administering the lie detector test does not know what group each subject is in.

Does this experiment have a control group? Is it blind, double-blind, or neither?

Try It Now Answers

1. The sample is the 20 fish. The population is all fish in the lake. The sample may be somewhat unrepresentative of the population since not all fish may be large enough to catch the bait.

2. This is a parameter, since the college would have access to data on all students (the population)

3. a. Categorical.

b. Quantitative

c. Quantitative

4. a. Systematic

b. Stratified or Quota

c. Voluntary response

d. Simple random

5. a. Response bias – historically, men are likely to over-report, and women are likely to under-report to this question.

b. Voluntary response bias – the sample is self-selected

c. Sampling bias – the sample may not be representative of the whole class

d. Lack of anonymity

e. Self-interest study

f. Loaded question

6. a. Observational study

b. Experiment; the treatment is the jumping jacks

c. Experiment; the treatments are coffee and tea

7. The truth-telling group could be considered the control group, but really both groups are treatment groups here, since it is important for the lie detector to be able to correctly identify lies, and also not identify truth-telling as lying. This study is blind since the person running the test does not know what group each subject is in.

3. Levine JD, Gordon NC, Smith R, Fields HL. (1981) Analgesic responses to morphine and placebo in individuals with postoperative pain. Pain. 10:379-89.

Explore with Wolfram|Alpha

More things to try:

• characteristic polynomial {{4,1},{2,-1}}
• maximize x(1-x)e^x

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Experiment." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/Experiment.html

Subject classifications